Sum Linked List Numbers Solution

Solution

Approach 1: Elementary School Math

Intuition

Keep track of the carry digit using an extra variable and follow simple digits-by-digits addition starting from the head of each list, since it should contain the least-significant digit.

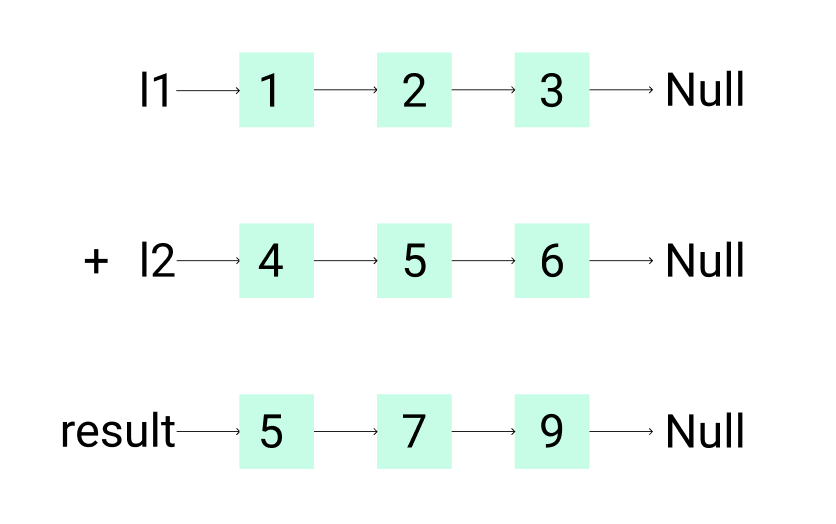
Figure 1. Visualization of the addition of two numbers: 321 + 654= 975. Each node contains a single digit and the digits are stored in reverse order.

Algorithm

Just like how you would sum two numbers on a piece of paper, we begin by summing the least-significant digits, which is the head of l1 and l2. Since each digit is in the range of 0 to 9, summing two digits may "overflow". For example: 6 + 8 = 14. In this case, we set the current digit to 4 and bring over the carry = 1 to the next iteration. The carry must be either 0 or 1 because the largest possible sum of two digits (including the carry) is 9 + 9 + 1 = 19.

The pseudocode is as follows:

• Initialize the current node to dummy head of the returning list.
• Initialize carry to 0.
• Initialize p and q to be the head of l1 and l2 respectively.
• Loop through lists l1 and l2 until you reach both ends. Set x to node p's value. If p has reached the end of l1, set to 0.
  Set y to node q's value. If q has reached the end of l2, set to 0.
  Set sum = x + y + carry.
  Update carry = sum / 10.
  Create a new node with the digit value of sum % 10 and set it to the current node's next, then advance the current node to next.
  Advance both p and q.
• Check if carry = 1, if so append a new node with digit 1 to the returning list.
• Return dummy head's next node.

Note that we use a dummy head to simplify the code. Without a dummy head, you would have to write extra conditional statements to initialize the head's value.

Take extra caution of the following cases:

Test case Explanation
l1=[0,1] l2=[0,1,2] When one list is longer than the other.
l1=[] l2=[0,1] When one list is null, which means an empty list.
l1=[9,9] l2=[1] The sum could have an extra carry of one at the end, which is easy to forget.

Complexity Analysis

• Time complexity : O(max(m, n)). Assume that m and n represent the length of l1 and l2 respectively, the algorithm above iterates at most max(m, n) times.
• Space complexity : O(max(m, n)). The length of the new list is at most max(m,n) + 1.

Follow up

What if the the digits in the linked list are stored in non-reversed order? For example:

(3 -> 4 -> 2) + (4 -> 6 -> 5) = 8 -> 0 -> 7